[Paper (p)review] Quantum Computation of Molecular Geometry via Many-body Nuclear Spin Echoes – Did we just enter an era of practical Quantum Computing?

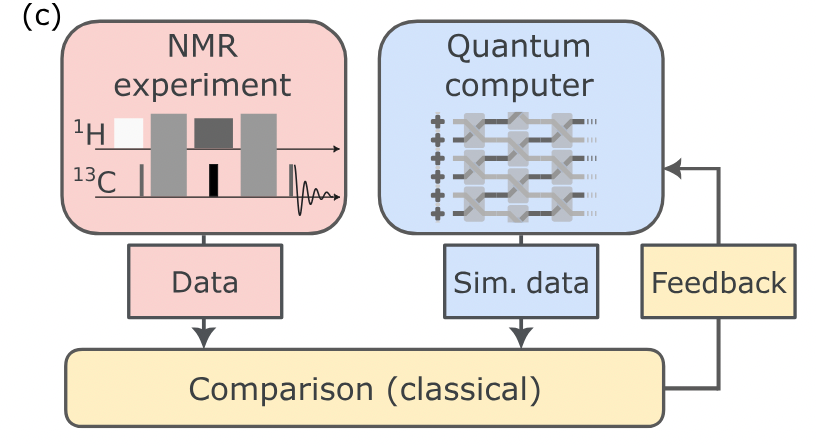
The idea of using a quantum computer as a simulator goes back to the great R. P. Feynman. Yet, 40 years later, practical applications of this idea appeared to be far from materializing.

It seems this changes now, with the work of the Google Quantum AI team and collaborators. A new pre-print “Quantum computation of molecular geometry via many-body nuclear spin echoes” (and its recently published precursor on OTOCs) is a proof-of-concept demonstration that a quantum computer can help compute quantities of other quantum systems that are too complex to be simulated classically. The idea behind the work is not new either. Even inside the Google AI team, it has been on the table almost three years ago as proven by the talk by Tom O’Brien (the last author of the latest pre-print):

The main point is to use the quantum computer as a digital twin of a target quantum system – here, molecules like toluene and DMBP suspended in liquid crystals – whose parameters (like shape or bond distances) are difficult to compute. Similarly to other applications of emulators known from engineering, like wind tunnels or driving simulators, the goal is to calibrate the digital twin until its response to a particular stimulus matches the response of the target system. Once the responses match, the parameters of the digital twin can be read out as the parameters of the target system. This contrasts with industrial digital twins often used for optimization and prediction, highlighting a use for parameter estimation.

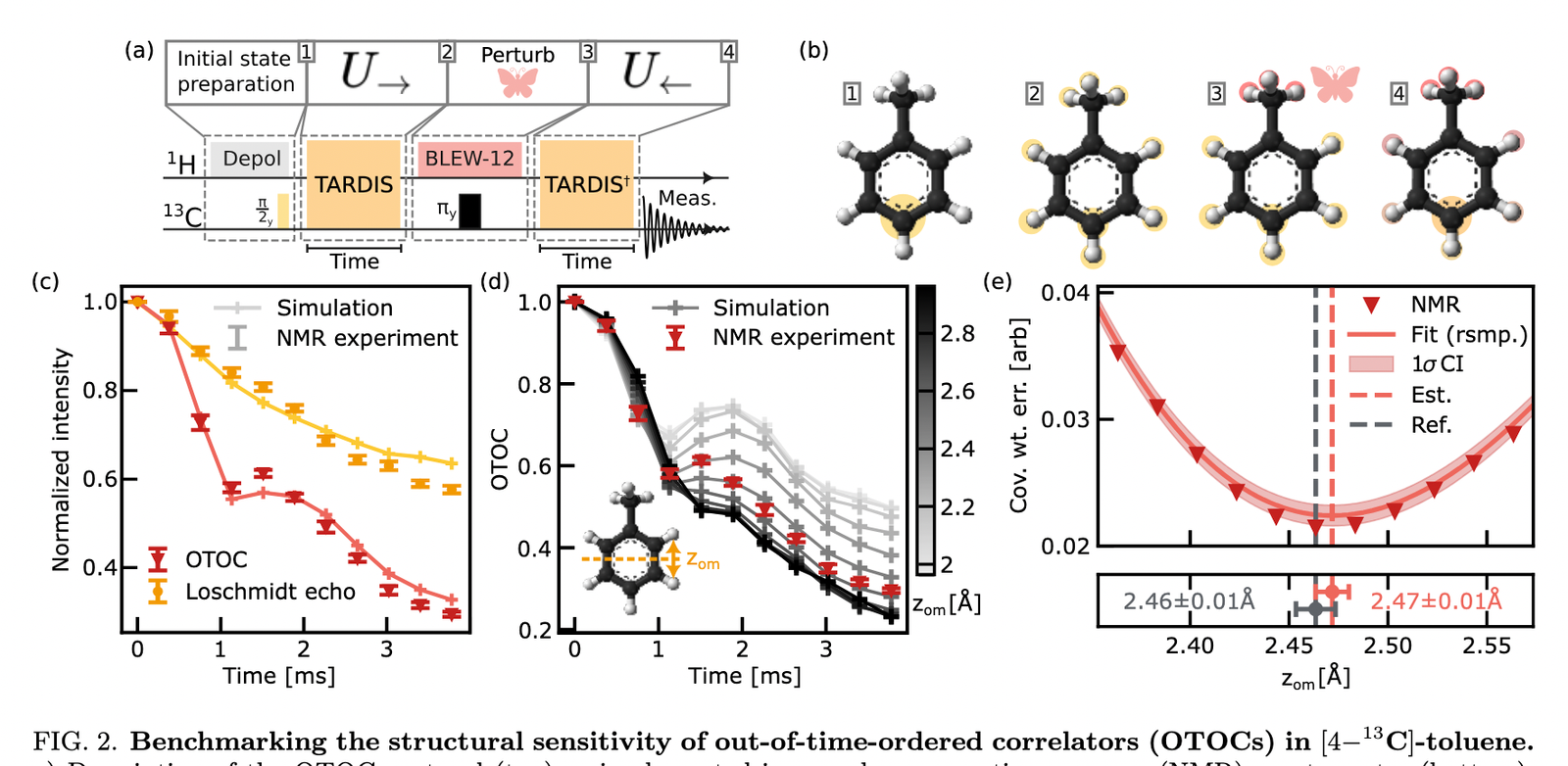
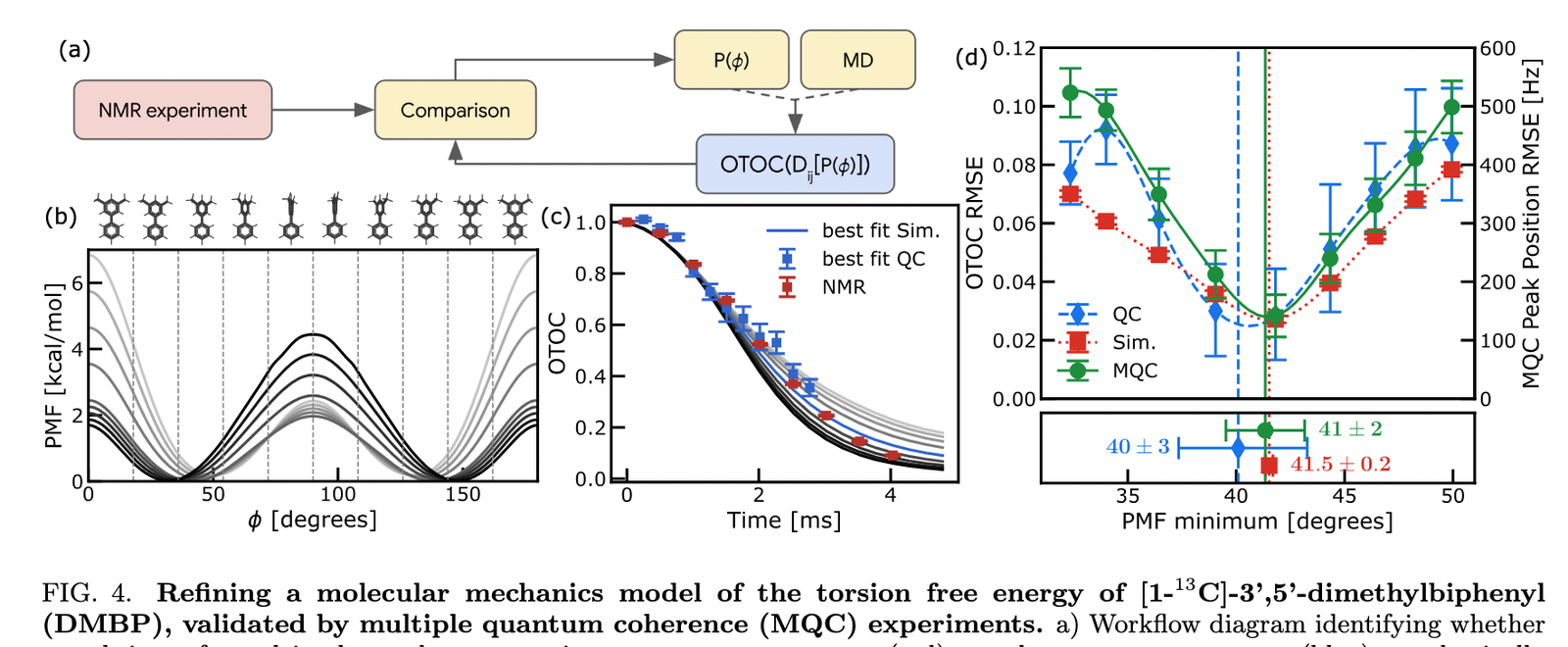
Two main results of the new pre-print

Sounds good in theory, but there are several challenges to overcome:

1. Stimulus and Response: The stimulus has to be experimentally realizable on both the target system (the molecule in an NMR machine) and the digital twin (the quantum computer circuit). The response has to be measurable on both systems as well. Plus, the response needs to be sufficiently rich to avoid ambiguities. Here, the stimulus involves specific NMR pulse sequences (like TARDIS) including a local perturbation (a “butterfly” pulse on methyl protons using BLEW12), and the response is the out-of-time-order correlator (OTOC), measured via the signal on a C13 nucleus. The OTOC measures how fast quantum information scrambles, and it’s known to be a very rich signal, making it suitable for this purpose.
2. Time Inversion: Measuring the OTOC requires effectively running time backward. This is easier on a quantum computer (implementing U^+) than on a real system. Here, the target system is probed using NMR, where time inversion can be cleverly achieved by “refocusing” techniques using engineered Hamiltonians, like the TARDIS pulse sequence does.
3. False Positives: If the response signal is too simple, multiple sets of parameters in the digital twin could match it, leading to wrong estimates. Here, the richness of the OTOC decay curve helps. The authors further reduce ambiguity by using multiple datasets (e.g., measuring toluene OTOCs with different added magnetic fields) and performing cross-validation (checking the DMBP result with a different NMR method, MQC spectroscopy)
4. Expressive Power of the Digital Twin: The digital twin has to be capable of reproducing the target system’s response. The idea is to model the known physics. Here, the target molecules (toluene simulated with 9 qubits, DMBP with 15) have complex interactions (dipolar couplings). The digital twin simulates this using a Trotterized evolution of the effective Hamiltonian, implemented with native quantum gates (like arbitrary-angle fSim gates or CZ gates) on Google’s Willow quantum processor. The specific circuits were even optimized using an AI algorithm called AlphaEvolve.
5. Optimization: Finding the right parameters for the digital twin involves a classical computer iteratively adjusting the simulation based on how well it matches the real NMR data. This hybrid quantum-classical loop minimizes a cost function (like the error between the simulated and real OTOC), similar in spirit to Variational Quantum Eigensolver (VQE) approaches. This requires running the quantum circuits many times, which is costly – but standard for near-term algorithms.
6. Noise Resilience: Both the NMR experiment and the quantum computer are noisy. The optimization must work despite this. On the digital twin side, the authors used a sophisticated four-stage error mitigation pipeline. This included techniques like Zero-Noise Extrapolation (ZNE) specifically adapted using a Pauli path model, along with light cone filtering, dynamical decoupling, twirling, and readout correction. This allowed them to achieve a final simulation error (RMSE) around 0.05.
7. Calibration and Validation: How do you check the answer if the target system is too complex to simulate classically? Here, the authors validated their results rigorously. For toluene, they compared their learned H-H distance to known values from literature. For DMBP, they measured the dihedral angle distribution using a different, costly experimental technique – Multiple Quantum Coherence (MQC) spectroscopy – on a specially prepared sample, finding good agreement.
8. Scalability: Can this approach work for larger, more interesting molecules? The classical cost of simulating OTOCs is the main bottleneck this work aims to overcome. While quantum OTOC simulation seems less costly than, say, electronic structure, simulating large, all-to-all coupled systems accurately still requires many gates. The authors estimate 1e5-1e6 gates might be needed for 50-60 spins using basic methods, highlighting the need for advanced quantum algorithms (like those found by AlphaEvolve). Encouragingly, they estimate OTOCs could probe long-range distances (20-60 Å), potentially offering advantages over traditional NMR methods.

To sum up, I believe the paper is a significant step towards practical quantum simulation. To me, however, this is not the end of the road, but rather the beginning of a new paradigm for quantum simulation, where the quantum computer is used as a learning machine – learning from real quantum systems, rather than just simulating abstract models. This opens exciting perspectives for novel applications of parameter learning (Bayesian learning, quantum machine learning), gradient-free optimization, response theory, and so on. I personally find this paper stimulating and exciting, with many ideas to explore further.

Paper on arXiv: https://arxiv.org/abs/2510.19550
OTOC paper: https://www.nature.com/articles/s41586-025-09526-6
Google blog: https://blog.google/technology/research/quantum-echoes-willow-verifiable-quantum-advantage/